Given,
The radius of curvature of the mirror $(R) = 1.27\;m = 127\;cm$
∵ $f = \frac{R}{2} = \frac{127}{2} = 63.5 \;cm$
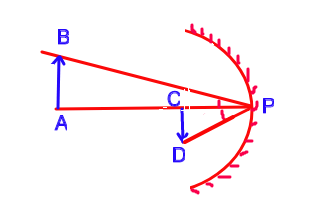
When an object falls from infinity, its image will be formed on the focal plane as shown in the figure below.
From $\Delta ABP,$ we have
$\tan \theta = \frac{2.54}{254}$ .......... (i)
From $\Delta CDP,$ we have
$\tan \theta = \frac{CD}{CP} = \frac{I}{f} = \frac{I}{63.5}$ .......... (ii)
From equation (i) and (ii), we get
$\frac{2.54}{254} = \frac{I}{63.5}$
$\Rightarrow \;\; I = \frac{2.54}{254} * 63.5 = 0.635\; cm$
$\therefore$ Diameter of the image is $I = 0.635\;cm$
Return to Main Menu