Return to Main Menu
Showing posts with label Physics Note. Show all posts
Showing posts with label Physics Note. Show all posts
Rotational Dynamics | Assignments
Assignment 1:
1. Three mass points $m_1$, $m_2$ and $m_3$ are located at the vertices of an equilateral triangle of length $a$. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through $m_1$?
2. Four particles of masses $4\;kg$, $2\;kg$, $3\;kg$ and $5\;kg$ are respectively located at the four corners $A$, $B$, $C$ and $D$ of a square of side $1\;m$. Calculate the moment of inertia of the system about:
(i) an axis passing through the point of intersection of the diagonals and perpendicular to the plane of the square,
(ii) the side $AB$,
(iii) the diagonal $BD$.
Assignment 2:
3. A wheel is rotating at a rate of 1000 rpm & its kinetic energy is $10^6$ J. Determine the moment of inertia of the wheel about its axis of rotation.
4. Find (i) the radius of gyration & (ii) the MI of the rod of mass $100\; gm$ and length $100 \; cm$ about an axis passing through its center & perpendicular to its length.
5. Calculate the angular momentum of the earth rotating about its own axis. Mass of the earth is $5.98 * 10^{24}\; kg$, Mean radius of earth is $6.37 * 10^6\; m$, MI of the earth is $\frac{2}{5}MR^2$.
6. The moment of inertia od the wheel is $1000\; kgm^2.$ At a given instant, its angular velocity is $10 \; rad/s$. After the wheel rotates through an angle $100$ radians, the wheels angular velocity is $100\; rad/s$. Calculate (i) the torque applied on the wheel. (ii) the increase in rotational KE.
7. A ballet dancer stretches her arms to reduce her motion. Explain.
8. If earth contracts to half its radius, what would be the length of the day?
9. Explain why spokes are fitted in the cycle wheel.
10. A fan with blades takes longer time to come to rest than without the blades. Why?
11. If the earth is struck by meteorites, the earth will slow down slightly. Why?
Return to Main Menu
Scalar and Vector | Assignment
Assignment 1:
1. If $B$ is added to $A$, under what condition does the resultant vector have a magnitude equal to $A + B$? Under what conditions are the resultant vector equal to zero?
2. State triangle law of vector addition. Obtain an expression for the resultant of two vectors $P$ and $Q$ inclined at angle $\theta$.
3. State the parallelogram law of vector addition. Derive the magnitude and direction of the resultant vector.
4. Can the sum of two equal vectors be equal to either of the vectors? Explain.
Assignment 2:
1. If the scalar product of two vectors is equal to the magnitude of their vector product, find the angle between them.
2. The magnitude of two vectors are equal and the angle between them is $\theta$. Show that their resultant divides angle $\theta$ equally.
3. If B is added to A, under what condition does the resultant vector have a magnitude equal to A + B? under what conditions is the resultant vector equal to zero.
4. Two vectors $\vec{A}$ and $\vec{B}$ are such that $\vec{A} - \vec{B} = C$ and $A - B = C$. Find the angle between them.
5. If $\widehat{i}$, $\widehat{j}$ and $\widehat{k}$ are unit vectors along $x, y,z - $ axis respectively. Find $\widehat{i}$ . ($\widehat{j}$ $\times$ $\widehat{k}$).
6. A force (in Newton) expressed in vector notation as $\vec{F} = 2 \widehat{i} + \widehat{j} - 3 \widehat{k}$ is applied on a body so that the displacement produced in meter is given by $\vec{D} = \widehat{i} - 2 \widehat{j} - 3 \widehat{k}$. Express the result and nature of the work done.
7. Given two vectors $\vec{A} = 4 \widehat{i} + 3 \widehat{j}$ and $\vec{B} = 5 \widehat{i} - 2 \widehat{j}$. Find the magnitude of each vector.
8. Can the walking of the person be an example of resolution of vector?
9. Show that the flight is an example of composition of vectors.
10. Find the unit vector of $3 \widehat{i} + 7\widehat{j} - \widehat{k}$
Return to Main Menu
Physical Properties | Assignment Collection
1) Find the dimension formula of,
Density / Pressure / Work / Energy / Power / Gravitational Constant / Momentum ?
2) To find the time period of a simple pendulum, its time period (t) may depend upon (i) mass (m) of the pendulum (ii) the length (l) and (iii) acceleration due to gravity (g).
3) Convert 1 dyne into Newton.
4) Convert 500 erg into Joule.
$(P + \frac{a}{V^2}) (V - b) = RT$.
Where, $P$ = Pressure, $V$ = Volume, $R$ = Universal gas constant, $T$ = Absolute Temperature.
6) Is dimensionally correct equation necessarily physically correct? What about the dimensionally wrong equation?
7) A student writes $\sqrt{(\frac{R}{2 \; G\; M}})$ for escape velocity. Check the correctness of the formula by using dimensional analysis.
8) Find the dimensions of Planck’s constant (h) from the given equation: $\lambda = \frac{h}{p}$; where λ is wavelength and p is the momentum of photon.
9) Convert density of water 1 $g/cm^3$ (CGS-system) into $kg/m^3$ (MKS – system).
10) Check the correctness of the relation $h = \frac{2 \; T \; Cos \theta}{r\; \rho\; g}$, Where symbols have usual meaning.
Return to Main Menu
Short Answer types
1. What is the center of buoyancy and metacenter?
Center of Buoyancy: When a body is placed in a fluid, the fluid exerts an upward force which is called buoyant force. Center of buoyancy is the point at which the whole buoyant force acts upwards
If the vessel is floating upright, the center of gravity and the center of buoyancy are in the same line.
Meta Center: It is the line drawn through the center of buoyancy of a floating vessel and corresponding line through a new center of buoyancy when the vessel is tilted.
2. Can the walk of man be an example of a resolution of vector?
An example of the resolution of a vector is the way a person walks. When a person walks, he/she presses the ground obliquely, (i.e., at an angle to the ground) in the backward direction. The ground offers an equal and opposite reaction in the opposite direction. The vertical component of this reaction balances the weight of the person. The horizontal component helps the person to walk.
3. If you wet your hand and pick up an ice tray that is below $0^{\circ}C$, your hands may stick to it. This does not happen to wood, why?
In fact, since wood is not warmer than the environment (unlike your hand) it may be easier for this to happen with wood. (Explain it more).
4. Do you expect the gas in the cooking gas cylinder to obey the ideal gas equation?
No. Because,
1) In a cooking gas cylinder, the gas is kept at high pressure and at room temperature. Real gases behave ideally only at low pressure and high temperature.
2) Cooking gas is kept in liquid state inside the cylinder because liquid state does not obey the ideal gas equation.
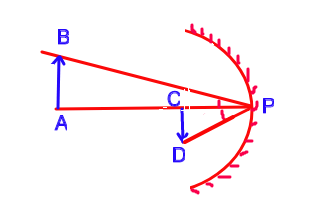
A coin 2.54 cm in diameter held 254 cm from the eye just covers the full moon. What is the diameter of the image of the moon formed by a concave mirror of radius of curvature 1.27 m?
Given,
The radius of curvature of the mirror $(R) = 1.27\;m = 127\;cm$
∵ $f = \frac{R}{2} = \frac{127}{2} = 63.5 \;cm$
When an object falls from infinity, its image will be formed on the focal plane as shown in the figure below.
From $\Delta ABP,$ we have
$\tan \theta = \frac{2.54}{254}$ .......... (i)
From $\Delta CDP,$ we have
$\tan \theta = \frac{CD}{CP} = \frac{I}{f} = \frac{I}{63.5}$ .......... (ii)
From equation (i) and (ii), we get
$\frac{2.54}{254} = \frac{I}{63.5}$
$\Rightarrow \;\; I = \frac{2.54}{254} * 63.5 = 0.635\; cm$
$\therefore$ Diameter of the image is $I = 0.635\;cm$
Return to Main Menu
Subscribe to:
Posts (Atom)