A coin 2.54 cm in diameter held 254 cm from the eye just covers the full moon. What is the diameter of the image of the moon formed by a concave mirror of radius of curvature 1.27 m?

Given, 

The radius of curvature of the mirror $(R) = 1.27\;m = 127\;cm$

∵ $f = \frac{R}{2} = \frac{127}{2} = 63.5 \;cm$

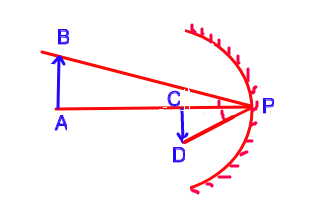
When an object falls from infinity, its image will be formed on the focal plane as shown in the figure below.

 

From $\Delta ABP,$ we have

$\tan \theta = \frac{2.54}{254}$ .......... (i)

From $\Delta CDP,$ we have

$\tan \theta = \frac{CD}{CP} = \frac{I}{f} = \frac{I}{63.5}$ .......... (ii)

From equation (i) and (ii), we get

$\frac{2.54}{254} = \frac{I}{63.5}$

$\Rightarrow \;\; I = \frac{2.54}{254} * 63.5 = 0.635\; cm$

$\therefore$ Diameter of the image is $I = 0.635\;cm$

Return to Main Menu