E1.5 Collisions (Elastic and Inelastic):

Collisions: 'two things hitting each other.'

---

A collision occurs when two or more objects hit each other. When objects collide, each object feels a force for a short amount of time. This force imparts an impulse, or change the momentum of each colliding objects.

But if the system of particles is isolated, we know that momentum is conserved. Therefore, while the momentum of each individual particle involved in the collision changes, the total momentum of the system remains constant.

In physics, a collision has two aspects: 

i) Two particles hit each other 

ii) A large force is felt by each particle for a relatively short amount of time.

---

The procedure for analyzing a collision depends on whether the process is Elastic or Inelastic Collision.

1) Elastic Collisions

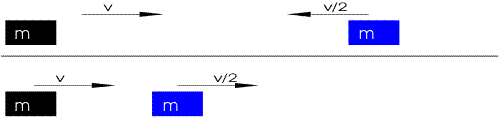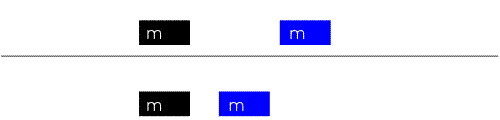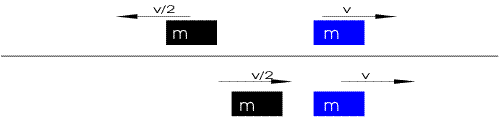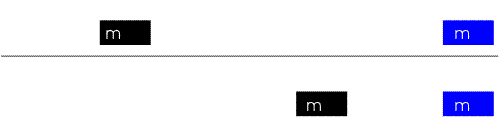
A collision between two or more bodies in which both momentum and kinetic energy are conserved. That is, there is no wasting of energy before and after collision.

An elastic collision is a collision between two or more bodies in which the total kinetic energy of the bodies before the collision is equal to the kinetic energy of the bodies after the collision. An elastic collision is not occur if kinetic energy is converted into other forms of energy. 

For example: Collision between fundamental particles (electrons, protons, neutrons), collisions between gas molecules etc.

Consider $m_1$ and $m_2$ be the masses of the particles having initial velocities $u_1$ & $u_2$ and $v_1$ and $v_2$ be the final velocities.

For this collision,

» $m_1\,u_1 + m_2\,u_2 = m_1\,v_1 + m_2\,v_2$ .......... (Conservation of Momentum)

» $\frac{1}{2}\,m_1\,u{_1}^2 + \frac{1}{2}\,m_2\,u{_2}^2 = \frac{1}{2}\,m_1\,v{_1}^2 + \frac{1}{2}\,m_2\,v{_2}^2$ .......... (Conservation of Kinetic Energy)

2) Inelastic Collisions:

An inelastic collision, the colliding particles strike together and move with common velocity as shown in figure. When two bodies collide and do not bounce away from each other, inelastic collision occurs.

In inelastic collision, momentum is conserved because the total momentum of both objects before and after the collision is same. 

But the kinetic energy is not conserved. Some of the kinetic energy is lost in the form of heat energy, sound energy, light energy etc. The most of the collisions in nature are inelastic. For Example: collisions between two cars, Mud thrown onto the wall etc.

For this collision,

» $m_1\,u_1 + m_2\,u_2 = (m_1 + m_2)\,v$

Where, $m_1$ and $m_2$ are the masses of the particles. $u_1$ and $u_2$ are their initial velocities and $v$ be the velocity after collision (i.e. common velocity).

Return to Main Menu