1.11 Simple Harmonic Motion (Simple Pendulum):

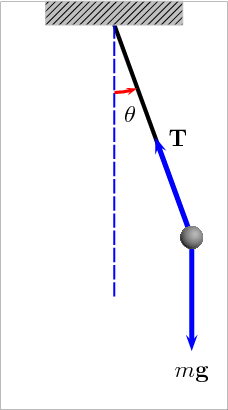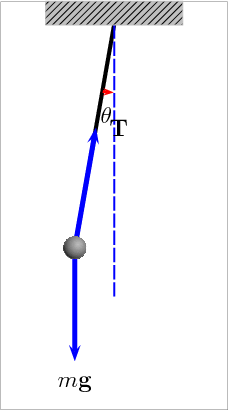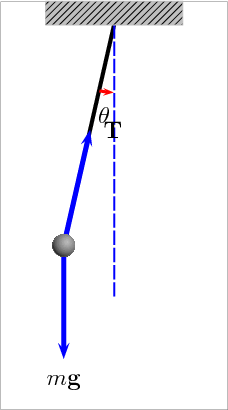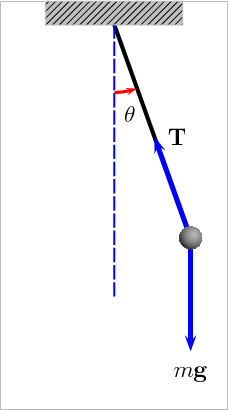
A simple pendulum is a heavy point mass suspended by an inextensible, weightless string from a rigid support. The pendulum oscillates in a vertical plane about the point of suspension as shown in the figure below.

Let $m$ be the mass of small bob is suspended by a thread from the rigid support $XY$ as shown in the figure.

Let $A$ be the equilibrium position of the pendulum. If the bob is displaced $y$ from the equilibrium position by an angle $\theta$ to new position $B$ and then released, it oscillates simple harmonically about its equilibrium position over a fixed path $CAB$.

At position B, The bob is under the action of following forces,

i) The component $mg\;Cos\theta$ of its weight $(mg)$ which balances the tension $(T)$ on the string,

i.e. $mg \; Cos\theta = T$ .......... (i)

ii) The component $mg\;Sin\theta$ of its weight $(mg)$ which provides the restoring force,

i.e. $F = -\; mg \; Sin\theta$ .......... (ii) 

[$-\;ve$ sign indicates that restoring force acts opposite to displacement]

If $a$ is the acceleration of the bob towards mean position due to restoring force, then

$F = ma$ .......... (iii)

From equation $(ii)$ and $(iii)$, we get

⇒ $a = -\;g \; Sin\theta$ .......... (iv)

If $\theta \; ￫ \; 0$, the motion of the bob along the curve $CAB$ considered as straight line. In such condition,

$Sin\theta ≈ \theta ≈$ $ \frac{arc \; AB}{l} = \frac{y}{l}$ [∵  $arc \; AB = AB = BN = y$ (Linear displacement)]

or, $a = - \; g$ $ \frac{y}{l}$

or, $a = -$ $ \frac{g}{l}$$y$ .......... (iv)

Since, $\frac{g}{l}$ is a constant for a given pendulum at a given place.

$a ∝ -\; y$ .......... (v)

Since acceleration is directly proportional to the linear displacement from mean position. This shows that the motion of the simple pendulum is simple harmonic.

Further, for the Time Period of simple pendulum,

The acceleration of the any particle in SHM is given by,

$a = - \; \omega^2\; y$ .......... (vi)

Comparing equation $(v)$ and $(vi)$, we get

$\omega^2 =$ $ \frac{g}{l}$

$\omega = $ $\sqrt{\frac{g}{l}}$

$\frac{2 \pi}{T}$ $ =  $ $ \sqrt{\frac{g}{l}}$                           [∵ $\omega = \frac{2\pi}{T}$]

$T = 2\pi$ $ \sqrt{\frac{l}{g}}$ .......... (vii)

Thus, the time period of the simple pendulum is entirely depends on $l$ and acceleration due to gravity  $g$ at a place.

Return to Main Menu